Introducing Bayesian Networks

Introduction

Bayesian networks are graphical models that show how different variables are related and influence each other using a directed graph. Each variable is a node, and the connections between them represent dependencies described with probabilities. These networks are useful for reasoning under uncertainty, as they allow you to calculate the likelihood of specific outcomes given some evidence. Commonly used in decision-making, medicine, and machine learning, Bayesian networks help make sense of complex systems by combining data with prior knowledge.

This paper shows by an example how they support making decisions in the face of uncertainty.

The Example

Suppose a dreaded disease afflicts 1% of the population and has a harsh treatment that might kill the patient. Two different tests for the disease are available, with known true-positive and false-negative statistics. Based on the test results, the patient must decide whether to take the treatment. This entails looking at how a person’s test outcomes, such as positive or negative, combined with the treatment they receive, influence their likelihood of survival. 

Methodology

The structure of the Bayesian Network is shown in Figure 1. It shows that being sick affects the test results and survival if treated. Treated is an intervention that a patient may or may not take. 

The Bayesian Network

The Morbidity

Note we never know whether the patient is sick; it is just the probability of being sick. This can be determined using Bayes theorem with these statistics:

Prior	Sick	Well
Morbidity	0.01	0.99

Prior Statistics 1

Test 1	Sick	Well
Positive	0.95	0.05
Negative	0.08	0.92

Test 1 Statistics

Test 2	Sick	Well
Positive	0.98	0.02
Negative	0.02	0.98

Test 2 Statistics

The patient’s probability of having the disease, the morbidity, is shown below. Note that with only one test, the chances of having the disease have gone from 1% to 10.7%.  That is why practitioners would follow up with further diagnostic procedures, such as a second test. Also, as shown below, the probability of the morbidity with two positive tests is 85.5%. So, there is still a reasonable probability she is well.

Morbidity Probabilities

Mortality

To decide whether to undergo treatment, she needs to know her probability of not surviving the mortality. Again, we apply Bayes’ theorem using the statistics of the treatment outcome shown below. Notice that if a well-patient takes the treatment, there is a 20% chance the treatment alone will kill her. So, the decision to take the treatment is very consequential.

Sick	Treated	P(Alive)	P(Dead)
Well	Untreated	0.99	0.01
Well	Treated	0.8	0.2
Sick	Untreated	0.4	0.6
Sick	Treated	0.9	0.1

Treatment Outcome Statistics

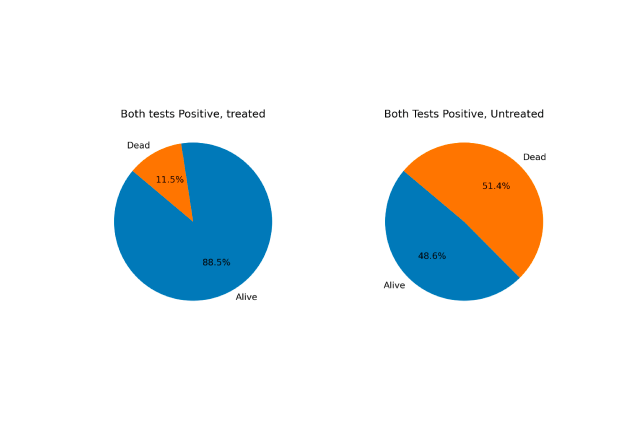
The results of the application of Bayes theorem are shown below.

Mortality Outcomes

The results are stark:

• With one positive test, the treatment will negatively impact her survival, actually going down from 92.7% to 81.1%, and so is inadvisable.
• With two positive tests, her survival chances significantly improved, going from 48.6% to 88.5%, so it is advisable to take the treatment.